Z-Score Calculator

Introduction Z-Score Calculator: Understanding and Using It with Examples

A Z-score calculator is a powerful statistical tool used to determine how many standard deviations an element is from the mean of a data set. Z-scores are essential in various fields, including finance, research, and education, as they provide a way to compare different data points within a distribution. In this article, we'll explore what a Z-score is, the formula used to calculate it, how to interpret the results, and provide detailed examples to illustrate its application.

What is a Z-Score?

A Z-score, also known as a standard score, is a numerical measurement that describes a value's relationship to the mean of a group of values. It is expressed in terms of standard deviations from the mean. A Z-score can be positive or negative, indicating whether the data point is above or below the mean, respectively.

In essence, the Z-score allows you to determine how unusual or typical a data point is within a given data set. If a Z-score is 0, it means the data point is exactly at the mean. A positive Z-score indicates the data point is above the mean, while a negative Z-score indicates it is below the mean.

Formula for Calculating Z-Score

The formula for calculating a Z-score is:

Z = (X - μ) / σ

Where:

• Z = Z-score
• X = Individual data point
• μ = Mean of the data set
• σ = Standard deviation of the data set

This formula subtracts the mean from the individual data point and then divides the result by the standard deviation. The Z-score tells you how many standard deviations the data point is from the mean.

Interpreting Z-Scores

Understanding Z-scores requires interpreting their values:

• Z = 0: The data point is exactly at the mean of the data set.
• Z > 0: The data point is above the mean.
• Z < 0: The data point is below the mean.
• Z > 1: The data point is more than one standard deviation above the mean, indicating it is higher than the majority of data points.
• Z < -1: The data point is more than one standard deviation below the mean, indicating it is lower than the majority of data points.

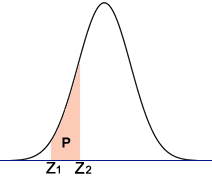
Z-scores can also be used to determine the percentile rank of a data point within a normal distribution. For instance, a Z-score of 1.96 corresponds to the 97.5th percentile, meaning that the data point is higher than 97.5% of the data in the distribution.

How to Use a Z-Score Calculator

Using a Z-score calculator involves a few simple steps:

1. Input the data point: Enter the value of the data point (X) you want to analyze.
2. Enter the mean: Input the mean (μ) of the data set.
3. Provide the standard deviation: Enter the standard deviation (σ) of the data set.
4. Calculate the Z-score: The calculator will use the formula to compute the Z-score.

The calculator will provide you with the Z-score, which you can then interpret to understand the position of the data point within the distribution.

Examples of Z-Score Calculations

Let’s go through some examples to better understand how to calculate and interpret Z-scores:

Example 1: Z-Score of a Test Score

Suppose a student scored 85 on a test where the mean score is 75 and the standard deviation is 10. To calculate the Z-score:

Z = (X - μ) / σ
Z = (85 - 75) / 10
Z = 10 / 10
Z = 1

The Z-score is 1, meaning the student scored one standard deviation above the mean.

Example 2: Z-Score in a Normal Distribution

Suppose the heights of adult men are normally distributed with a mean of 70 inches and a standard deviation of 3 inches. What is the Z-score for a man who is 74 inches tall?

Z = (X - μ) / σ
Z = (74 - 70) / 3
Z ≈ 1.33

The Z-score is approximately 1.33, indicating that the man is 1.33 standard deviations taller than the average height.

Example 3: Z-Score of a Negative Value

Consider a data set with a mean of 50 and a standard deviation of 5. If a data point in the set is 45, the Z-score is calculated as follows:

Z = (X - μ) / σ
Z = (45 - 50) / 5
Z = -5 / 5
Z = -1

The Z-score is -1, meaning the data point is one standard deviation below the mean.

Applications of Z-Score Calculations

Z-scores are widely used in various fields to standardize scores and make meaningful comparisons. Here are some common applications:

• Standardized Testing: Z-scores are used to compare individual test scores against the average, helping to identify how well a student performed relative to their peers.
• Finance: In finance, Z-scores are used in credit risk analysis, particularly in models like the Altman Z-score, which predicts the likelihood of a company going bankrupt.
• Quality Control: Z-scores are used in manufacturing and quality control to determine whether a product's dimensions or characteristics fall within acceptable limits.
• Health and Medicine: Z-scores are used in medical statistics, such as determining a child's growth percentile based on height or weight.
• Psychology: Z-scores are used in psychological testing to compare individual performance to a normative group.

Advantages of Using a Z-Score Calculator

There are several benefits to using a Z-score calculator:

• Accuracy: The calculator provides precise calculations, reducing the chance of manual errors.
• Efficiency: It saves time by quickly computing Z-scores for large data sets or complex distributions.
• Standardization: Z-scores standardize different data sets, making it easier to compare individual data points across different distributions.
• Educational Value: Helps students and professionals alike understand and apply statistical concepts in real-world scenarios.
• Convenience: The calculator is easy to use and accessible, requiring only basic inputs to generate results.

Limitations of Z-Score Calculations

While Z-scores are a valuable tool in statistical analysis, they do have some limitations:

• Assumption of Normality: Z-scores assume that the data follows a normal distribution, which may not always be the case.
• Relative Comparison: Z-scores only provide relative comparisons within the same data set and may not be applicable for different distributions.
• Outliers: Z-scores can be heavily influenced by outliers, leading to misleading results if the data set contains extreme values.

Conclusion

A Z-score calculator is an essential tool for anyone working with statistical data, whether in academia, finance, psychology, or any other field where comparing data points is crucial. By understanding how to calculate and interpret Z-scores, you can gain valuable insights into the relative position of individual data points within a distribution.

The examples provided in this article demonstrate the practical application of Z-scores and how they can be used to standardize and compare different data sets. While Z-scores have their limitations, they remain a powerful tool in statistical analysis, helping to make data more understandable and comparable.

Whether you're analyzing test scores, financial data, or psychological assessments, a Z-score calculator can help you quickly and accurately determine how far a data point deviates from the mean, providing a clear understanding of its relative position within the data set.